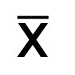Harmonic mean, another measure of central tendency, is one of the three Pythagorean means (the other two being arithmetic mean and geometric mean). This type of average is frequently used in situations where one is trying to calculate the average of rates. It is also commonly used in mathematics (geometry, trigonometry, and statistics), science (physics), and in finance.

Compared to the other Pythagorean means, the harmonic mean most commonly relates to the arithmetic mean. The history of harmonic means dates back to Greece where the Greeks commonly used them in music, to hold strings on instruments in certain ratios while plucking.

To calculate the harmonic mean for a set of a data, all of the individual elements are averaged and divided by the sum of the reciprocals of the elements. The formula for calculating harmonic mean is: N / (1/a1 + 1/a2 + 1/a3 + 1/a4 + ……. +1/aN) where N is the total sample size of your data.

For a working example, let’s analyze a set of data containing your miniature golf scores for the last 5 holes of your favorite course. The data set is as follows: [3,2,2,1,5]. Filled in with the values from your sample data, the equation for his harmonic mean would be: 5 / (1/3 + 1/2 + 1/2 + 1/1 + 1/5). The harmonic mean for this data set is 1.9763.

In a positive data set which contains at least one pair of non-equal values, the value of the harmonic mean will always be the lowest, the value of the arithmetic mean will always be the highest, and the value of the geometric mean will always be in the middle between the other two.

To use our harmonic mean calculator, simply input your data set with values separated by commas and no spaces. For this example, you would input: 3,2,2,1,5.