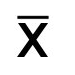Geometric mean, one of the three Pythagorean means, is another type of average used to help characterize the central tendency of a set of numbers in math, science, and finance. While lesser known than the arithmetic mean, the geometric mean is an important calculation often used by scientists, biologists, and in financial reporting.

The geometric mean is calculated by multiplying a set of numbers and taking the nth root, where n represents the total number of values in the sample. If that sounds like a mouthful, it can be simplified by thinking of it as the average of the logarithmic values converted into a base 10 number. The basic formula for calculating geometric mean is: ((X1)(X2)(X3)……..(XN))1/N.

The geometric mean can only be applied to positive numbers and it is often used with numbers and figures that are meant to be multiplied together or that grow exponentially. It’s for this reason that it makes a popular choice when calculating averages in finance or studying things like population growth.

For a simple working example, let’s pretend we’re analyzing a set of data that contains the number of sodas you drank each day for the last four days. The data set is as follows: [1,3,2,2]. To find the geometric mean of this data, we would insert our values into the geometric mean equation, with n being 4 (the total sample size), which would produce the following: ((1) x (3) x (2) x (2))1/4. The geometric mean for this data is 1.8612.

To use our geometric mean calculator, simply input your data values separated by commas with no spaces, such as: 1,3,2,2. This calculator is useful because geometric mean calculations often result in large numbers and are easy to lose track of.